Тригонометрические уравнения это задании №13 с развернутым ответом. Оно относится к заданиям повышенной сложности. При верном решении за него можно получить до 6 баллов. «Подводных камней» в этом задании не так много, но они все же есть. На что надо обращать внимание, чтобы не потерять такие нужные баллы?
Первое, на что надо смотреть необходима ли область определения уравнения. Ее надо обязательно записать, если есть корень, дробь или функции tg x или ctg x. По сути, область определения tg x и ctg x тоже можно свести к дроби, т.к. tg x это отношение sin x к cos x, а ctg x отношение cos x к sin x.
Пример 1. уравнение
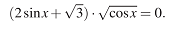
В этом уравнении cos x стоит под корнем, значит, его значения должны быть больше или равны нулю.
Пример 2
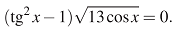
Здесь cos x стоит под корнем и есть tg x. Cos x ≥0, x≠πn, n-целое число.
С областью определения уравнения разобрались, можно приступать к решению. Для тех, кто приступает к решению заданий с развернутым ответом, не стоит говорить о том, что основные формулы надо знать наизусть. Справочного материала в профильных вариантах крайне мало. Есть основное тригонометрическое тождество, формулы двойного угла для sin x и cos x, формулы синуса и косинуса суммы аргументов. Пригодится еще знание формул приведения. Формулы приведения можно не заучивать наизусть, а просто помнить правило: если делится на 2, то функцию меняем на сходственную, если не делится функцию оставляем неизменной. Знак определяем по знаку исходной функции.
Решение тригонометрических уравнений сводится к тому, что надо прийти к одной функции и одному аргументу. Для этого используем формулы двойного угла, суммы и разности аргументов, приведения, связь между тригонометрическими функциями.
Чаще всего при решении тригонометрических уравнений используют метод разложения на множители или замены переменной.
Вторая часть 13-го задания заключается в выборе корней, удовлетворяющих определенному условию: «найдите корни, принадлежащие отрезку…»
Для определения корней, принадлежащих заданному отрезку, можно выбрать один из трех способов. Первый графический. Строим числовую окружность, отмечаем корни. Ограничиваем отрезок и выбираем те корни, которые принадлежат отрезку. Этот способ наименее популярный.
Второй способ метод перебора. Задаем значения n: 0; 1; -1;… Вычисляем корни и выбираем нужные. Здесь важно показать, что выбрали все корни. Например, если дан отрезок от 0 до то надо получить первый отрицательный корень и первый корень, больший Третий метод метод двойного неравенства. Здесь все делается просто, полученные корни подставляем в заданный нам промежуток.
Пример: пусть задан промежуток [–7π/2; –2π], корень π/2 πn. Находим целые значения для n.
–7π/2 π/2 πn –2π
Сразу делим все на –7/2 1/2 n –2
–7/2 1/2 n –2 1/2
–4 n –5/2
Целые n в этом промежутку это –4 и –3. Значит корни принадлежащие этому промежутку буду π/2 π(–4) –7π/2, π/2 π(–3) –5π/2.
Получить максимальный балл за тригонометрические уравнения не так сложно. Важно только помнить формулы и быть внимательным.
Ваша Дарья Круглова